Buffer Mathematics

Updated on December 2024

The Difference Between Thermodynamic pKa and Apparent pKa

A buffer species with a single protonated state is defined as

HA^{z+1} \rightleftharpoons H^+ + A^z

(1)

where $HA$ is a weak acid, $A$ the conjugate base, and $z$ the charge of the conjugate base.

It follows that the dissociation constant is defined as

K_a = \frac{[H^+] [A^z]}{[HA^{z+1}]}

(2)

The dissociation constant, $K_a$ , is however more commonly presented as its own negative logarithm

pK_a = -log(K_a)

(3)

Substituting and rearranging, we get that

pK_a = pH -log\bigg(\frac{[A^z]}{[HA^{z+1}]}\bigg)

(4)

However, this is only true under ideal conditions. In reality, many non-idealities exist. For example, any free ion $X$ would be shielded by oppositely charged ions in the solution. This changes the apparent concentration of $X$ . It can be said that the activity of $X$ changes. The activity is therefore defined as

a_X = \gamma_X[X]

(5)

where $a_X$ is the activity, $\gamma_X$ is the activity coefficient, and $[X]$ is the concentration of $X$ , respectively.

Substituting the concentrations with the corresponding activities in equation (4), we get that

pK_a' = pH -log\bigg(\frac{a_A}{a_{HA^{z+1}}}\bigg) = pH - log\bigg(\frac{\gamma_A[A]}{\gamma_{HA}[HA]}\bigg)

= pH - log\bigg(\frac{[A]}{[HA]}\bigg) - log\bigg(\frac{\gamma_A}{\gamma_{HA}}\bigg)

(6)

and thus

pK_a' = pK_a - log\bigg(\frac{\gamma_A}{\gamma_{HA}}\bigg)

(7)

where $pK_a'$ is the apparent pKa under specific conditions, and $pK_a$ is the thermodynamic pKa, determined at ideal conditions.

The activity coefficients vary widely for different species and under different conditions and must be determined experimentally.

How Ionic Strength Influences Apparent pKa

The presence of ions changes the activity of any acid-base pair. However, different acids are more affected than others.

The ionic strength of a solution is defined as

I = \frac{1}{2} \sum_{i=1}^{n} c_i z_i^2

(8)

where $c_i$ is the concentration of ion $i$ , and $z_i$ is the charge of ion $i$ .

Empirical correlations between the activity of an acid-base pair and the ionic strength of the solution have been determined [1], and substituting this into equation (7) we get that

pK_a' = pK_a + (2z+1) \beta\frac{\sqrt{I}}{1+\sqrt{I}} - 0.1I

(9)

where $z$ is the charge of the conjugate base and

\beta = 1.825 \times 10^6 \times (\varepsilon T)^{-3/2}

(10)

and

\varepsilon = 87.7 - 0.400(T_C) + 9.40 \times 10^{-4}(T_C)^2 - 1.41 \times 10^{-6}(T_C)^3

(11)

where $T$ is the temperature in Kelvin and $T_C$ is the temperature in Celsius [2].

Equation (9) finally allows us to study how the ionic strength of the solution affects the buffer acid's pKa'. From equation (9), we see that for acids with a neutral or a positively charged conjugate base, the pKa' increases with increasing ionic strength. Conversely, for acids with a negatively charged conjugate base pKa' decreases with increasing ionic strength.

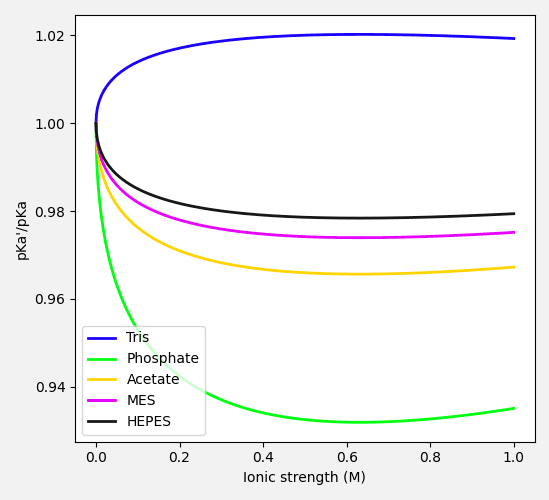
Figure showing difference between thermodynamic pKa and apparent pKa at different ionic strengths

When calculating pKa' in equation (9), it is important to recognize that the calculated pKa' affects the equilibrium ratio of the acidic and basic components of the buffer. This in turn leads to a change in total ionic strength of the solution, which subsequently affects the pKa'. It thus becomes an iterative problem to solve.

If you need to accuurately calculate the recipie to create a buffer of a certain pH, taking ionic strength from salt additives and temperature into account, you can use our free-to-use buffer calculator.

Buffer Mathematics

The Difference Between Thermodynamic pKa and Apparent pKa

How Ionic Strength Influences Apparent pKa

References